Calendar and continued fractions

The idea of a modern calendar is to have a cycle spanning several years some of which are leap years while the others are not, with the mean year length being as close to the astronomical year as possible. The cycle length should be either very short or very easy to use. For example the Julian 4 year cycle is nice as well as Gregorian 400 year cycle. The Hebrew 19 year cycle requires a calculator to figure out the leap years (where an extra month, not day, is added). Suppose that we have a cycle of $q$ years during which there are $p$ leap years. Then during the cycle $365q+p$ days pass. This makes the mean year length to be $365+p/q$ days. Let $\alpha =0.24219878$. Then we need to find the small and ``nice'' $q$ making $p/q$ as close to $\alpha$ as possible. We already know that we need to examine the sequence of convergents coming from the continued fraction expansion of the number $\alpha$. For $\alpha =0.24219878$ we have $$0.24219878=\displaystyle \frac{1}{4 + {\displaystyle \frac{1......e \frac{1}{3 +{\displaystyle\frac{1}{5 + \ddots}} }} }} }} }$$

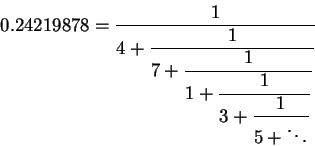
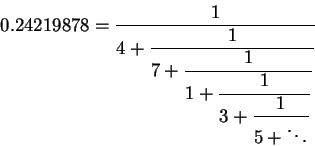
which gives the following sequence of convergents:

$$\frac{p_1}{q_1}=\mbox{${\displaystyle\frac{1}{4}}$},\ \frac{p......rac{p_4}{q_4}=\frac{31}{128},\\frac{p_5}{q_5}=\frac{163}{673}.$$

The first fraction in the sequence corresponds to the Julian 4 year cycle system with a single leap year in the cycle. The remaining fractions offer very inconvenient cycle lengths: 29, 33, 128 and 673 years respectively. They are, therefore, rejected. (Nevertheless, the idea of a 33-year period has crossed people's minds. Such a calendar would indeed be more precise than the current Gregorian calendar, but less precise than the 500-year cycle calendar disussed below.)
Instead, we would rather have a cycle several centuries long, i.e.$q=100q'$, where $q'$ must be an integer between 1 and 9. This corresponds to the problem of approximating the number $\alpha '=100\alpha =24.219878$ by rationals.

$$0.24219878\times 100 =24 + \displaystyle \frac {1}{4 + {\dis......e \frac {1}{1 + {\displaystyle \frac {1}{4 +\ddots}} }} }} }$$

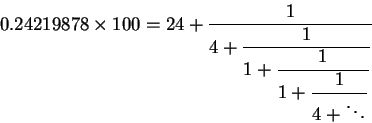
We easily compute first 4 convergents:

$$\frac{p_1}{q_1}=\frac{97}{4},\ \frac{p_2}{q_2}=\frac{121}{5},\\frac{p_3}{q_3}=\frac{218}{9},\ \frac{p_4}{q_4}=\frac{993}{41}.$$

We see that we have three candidates for the calendar model. The first one corresponds to our Gregorian calendar. It is based on a 400 year cycle with 97 leap years: all those divisible by 4 (there is a hundred of them) except 100th, 200th and 300th years making up the needed 97 leap years in a cycle. The next fraction 121/5 corresponds to a 500 year cycle calendar with 121 leap years in each cycle. In such a calendar every year divisible by 4 would be a leap year unless it is divisible by 100 with the exception of years divisible by 500, which are still leap years. This system is as simple and as convenient as the Gregorian calendar and provides a better accuracy. The Gregorian year is 26 seconds longer than the solar year resulting in 1 day error each 3,320 years. The 500 year cycle calendar is 17 seconds shorter than the solar year resulting in 1 day error each 5,031 years. The Pope missed that one. The last choice for the calendar offers a 900 year cycle. However, with 218 leap years in the cycle the calendar requires to make 7 exceptions to the fourth year leap rule $(218=900\div 4 -7)$. Making this arrangement would create a more complicated calendar. And besides, the 900 year cycle may be just a bit too long to be convenient. So, we would reject this more precise calendar in favor of the simpler ones.

This is the difference between our Gregorian calendar time and the true solar time over 100 years. The sawtooth oscillations are the insertions of leap years every four years. This is the difference between our Gregorian calendar time and the true solar time over 900 years. The individual leap year insertions are almost invisible. We clearly see the effect of leap year omissions every century and the effect of the leap year every 4 centuries. In fact, if we omit the 400 year rule but keep omitting leap years every century the calendar error will look like this: The green line shows the Gregorian calendar error for comparison.

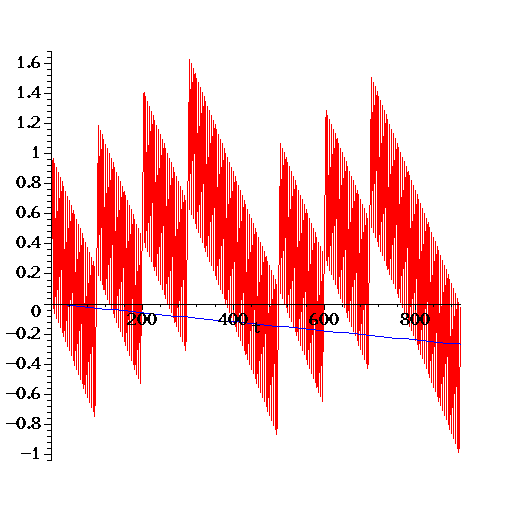
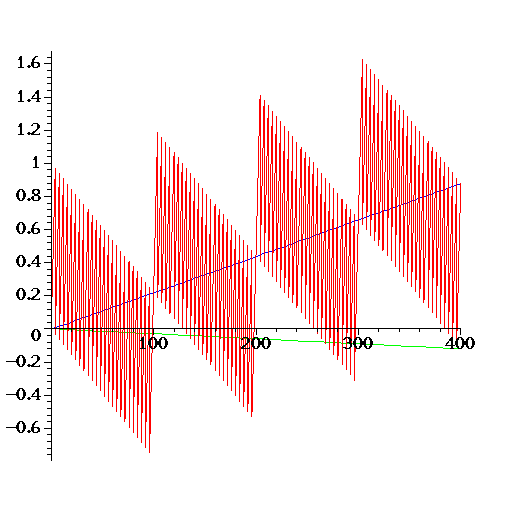
Even Gregorian calendar will accumulate a large error. Eventually.

Here the individual leap years are no longer visible. The smaller oscillations are centennial omissions of leap years. These are grouped into repeating packets of four. We see that our calendar accumulates error at the rate of about 1 day every 3,300 years.

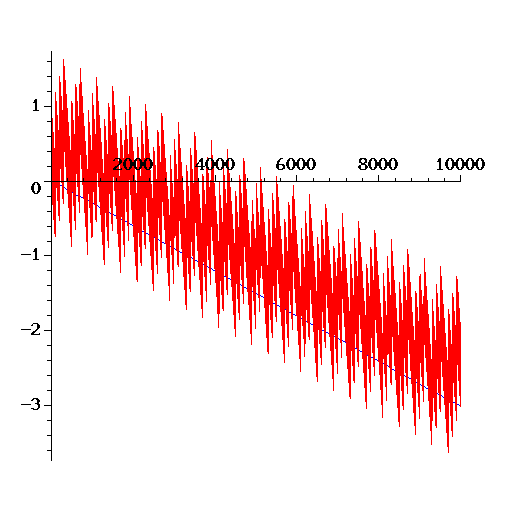
We might speculate what can be done in the future to correct for the slowly accumulating error of the Gregorian calendar. The idea is to keep the old system but make some very infrequent corrections. Continued fractions come handy here again. In other words we are looking for a much longer cycle length $q$ which would comprise several 400 year cycles: $q=400q'$, where $q'$ is the number of 400 year cycles in the new long cycle. We then expand $400\times 0.24219878$ into a continued fraction.

$$400\times 0.24219878=96 + {\displaystyle \frac {1}{1 + {\disp......e \frac {1}{3 + {\displaystyle \frac {1}{2 +\ddots}} }} }} }}$$

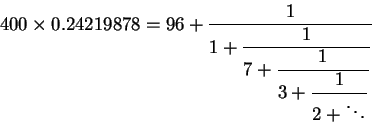
Convergents are 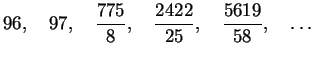$96, \quad 97, \quad {\displaystyle \frac {775}{8}} , \quad{\displaystyle\frac {2422}{25}} , \quad{\displaystyle \frac {5619}{58}},\quad\ldots$ The third convergent suggests a $8\times 400=3,200$ year cycle with $775$ leap years altogether. Recall, that according to the Gregorian calendar, there is $97$ leap years in each 400 year cycle. So, within 8 cycles we will have $8\times 97=776$ leap years. Thus, canceling the leap year every 3,200 years will allow us to keep Gregorian calendar in the intervening time, while making it much more precise. The new system would accumulate a 1 day error in 100,000 years, that is never.

An even more interesting scenario would have been possible had the Pope done his math. If our calendar was based on a 500 year cycle suggested above, then we would be expanding $500\times 0.24219878$ into a continued fraction.

$$500\times 0.24219878=121 + {\displaystyle \frac {1}{10 + {\d......c {1}{2 +{\displaystyle \frac {1}{2 + \ddots }} }} }} }} }}$$

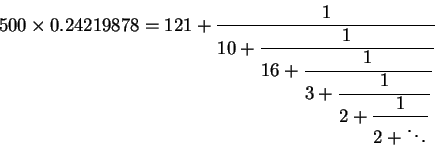
with convergents

$$[121, \,{\displaystyle \frac {1211}{10}} , \,{\displaystyle......{1147}} , \,{\displaystyle \frac {337504}{2787}} , \,\ldots ]$$

The second convergent $1211/10$ suggests a new cycle length of 5,000 years with 1211 leap years in the cycle. The 500 year cycle calendar would have 1210 leap years. In order to make 1211 leap years we might want to have February 5,000 have 30 days in celebration of the 5th millennium. The 5,000 year cycle calendar will accumulate a 1 day error in a whopping 1 million years. This system has been suggested by Bernard Rasof ("Continued fractions and 'leap' years", The Mathematics Teacher, 63, pp. 144-148, 445, 1970.) Be it as it may, either the Pope didn't do his math (which I find unlikely), or the astronomical data was not precise enough at the time to justify the 500 year cycle, or he had other reasons for settling on the current calendar (for example, the coming-soon 1600 would not increase the discrepancy between the two versions of the calendar under the 400 year cycle).

The continued fractions can also be used to discover the 19 year Metonic cycle of the Hebrew calendar. In lunar calendars an extra month (from new moon to new moon) is inserted in a leap year. As we mentioned in the beginning, there is 12.368267 lunations a year. Expanding this number into a continued fraction we obtain

$$12.368267=12 + {\displaystyle \frac {1}{2 + {\displaystyle \...... {1}{1 + {\displaystyle \frac {1}{17 +\ddots}} }} }} }} }} }}$$

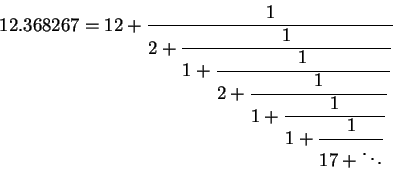
with convergents 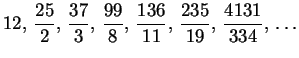$12, \,{\displaystyle \frac {25}{2}} , \,{\displaystyle \frac {37}{3}} , \,{\di......isplaystyle \frac {235}{19}} , \,{\displaystyle \frac {4131}{334}} , \, \ldots$

The Metonic cycle corresponds to the sixth convergent$$\frac {235}{19}$$ meaning that there is approximately 235 lunations in 19 years. If all years contained 12 months then in 19 years we would have $19\times 12=228$. Therefore, we need to insert 7 more months to make it to 235. The actual leap year rule requires a calculator: The year $Y$ is a leap year if $7Y+1\pmod{19}<7$.

If you want to learn more about continued fractions the books
Lang, Serge Introduction to Diophantine approximations. Second edition. Springer-Verlag, New York, 1995.
and
Jones, William B.; Thron, Wolfgang J. Continued fractions. Analytic theory and applications. With a foreword by Felix E. Browder. With an introduction by Peter Henrici. Encyclopedia of Mathematics and its Applications, 11. Addison-Wesley Publishing Co., Reading, Mass., 1980.
are excellent references.

The calendar history and continued fractions are also discussed in two Mathematical Intelligencer articles:
Dutka, Jacques "On the Gregorian revision of the Julian calendar", Math. Intelligencer 10 (1988), no. 1, 56--64.
and
Rickey, V. Frederick "Mathematics of the Gregorian calendar", Math. Intelligencer 7 (1985), no. 1, 53--56.

There is another web site that discusses both the calendar and the continued fractions. It focuses, however, more on the calendar part than on continued fractions.

Finally, I would like to mention that I got my idea for doing the public lecture about it on February 29, 2000 from an article in January/February 2000 issue of one of my favorite magazines Quantum.

The slightly altered version of this web page without the hypertext links can be downloaded as a PDF file.

2000-03-03