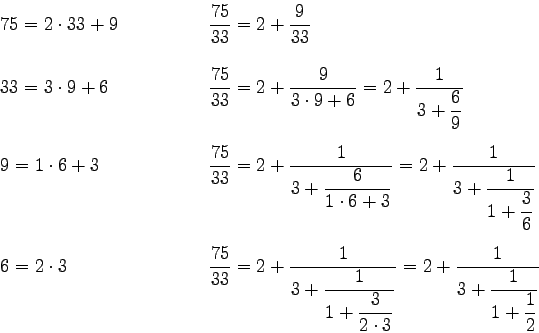
Let us recall this algorithm. Suppose we would like to find the greatest common divisor of numbers 75 and 33.
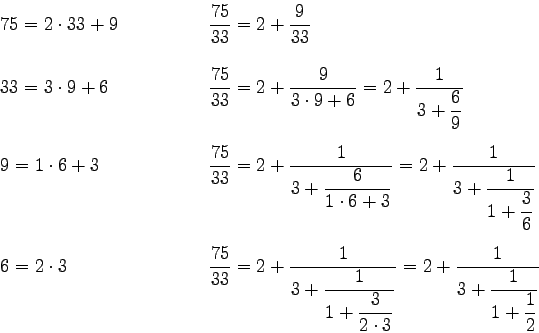
The last non-zero remainder, 3 in our case, is the greatest common divisor of 75 and 33.
There is no evidence though that Greeks knew about the connection between
the left column and the right column above. The first continued fraction
was used in 1572 by Bombelli to approximate ![]() .
The first infinite continued fraction appears in 1659 in the work of Lord
Brouncker to expand
.
The first infinite continued fraction appears in 1659 in the work of Lord
Brouncker to expand ![]() .
It is Euler's
systematic
development of the theory starting in 1737 that showed the value of the
notion for both number theory and analysis. A torrent of results followed.
In 18th and 19th centuries everybody who was anybody in mathematics contributed.
.
It is Euler's
systematic
development of the theory starting in 1737 that showed the value of the
notion for both number theory and analysis. A torrent of results followed.
In 18th and 19th centuries everybody who was anybody in mathematics contributed.
If the number is rational the continued fraction terminates like for ![]() .
If the number is irrational the continued fraction goes on forever. For
example, for the irrational number
.
If the number is irrational the continued fraction goes on forever. For
example, for the irrational number ![]() we can execute the Euclidean algorithm, in essence looking for the greatest
common divisor of
we can execute the Euclidean algorithm, in essence looking for the greatest
common divisor of ![]() and
and ![]() .
The algorithm will never terminate since the two numbers are incommensurate.
.
The algorithm will never terminate since the two numbers are incommensurate.
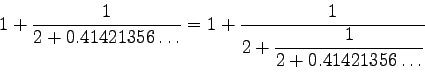
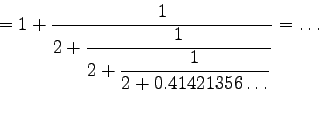
concluding

The esthetic beauty of continued fractions may go some ways towards justifying the significance of some numbers from algebra or geometry. The continued fraction expansion
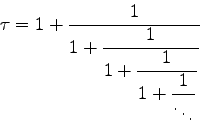
would suggest that the number ![]() has some significance. In fact, this number is none other than the ``golden
ratio''.
has some significance. In fact, this number is none other than the ``golden
ratio''.
If we terminate the infinite continued fraction for the irrational number ![]() at the
at the ![]() th
step we will obtain a rational approximation
th
step we will obtain a rational approximation ![]() to
to ![]() .
The rational number
.
The rational number ![]() is called the
is called the ![]() th
convergent for
th
convergent for ![]() .
For example, the first 4 convergents to numbers
.
For example, the first 4 convergents to numbers ![]() and
and ![]() are
are
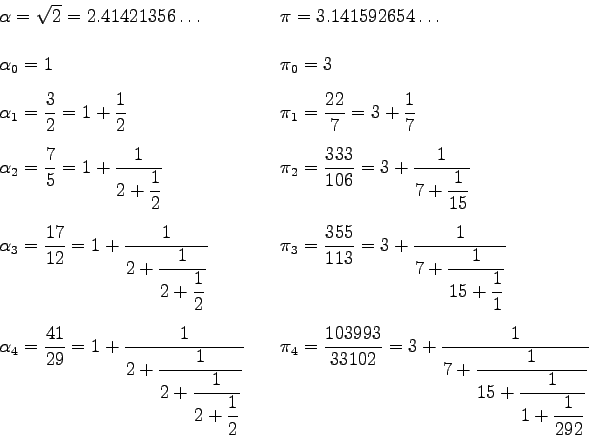
The name convergent comes from the fact that convergents do converge to the number. For example,
Here is the graph for ![]() .
.
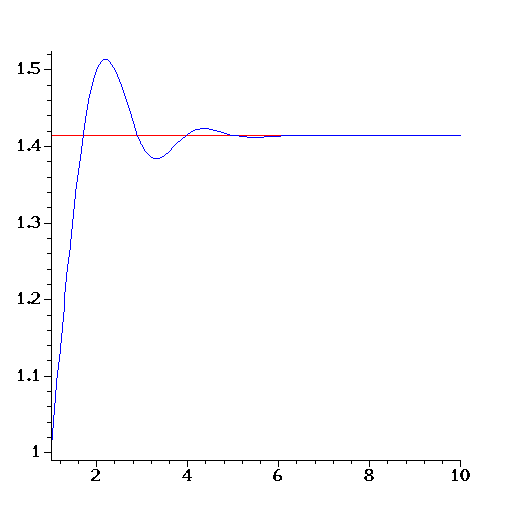
Here is the graph for ![]() .
.
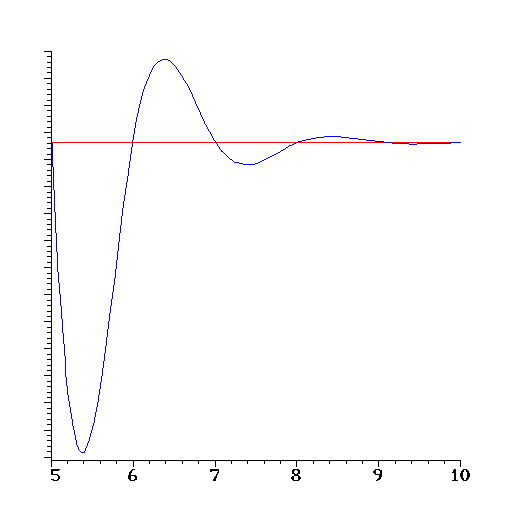
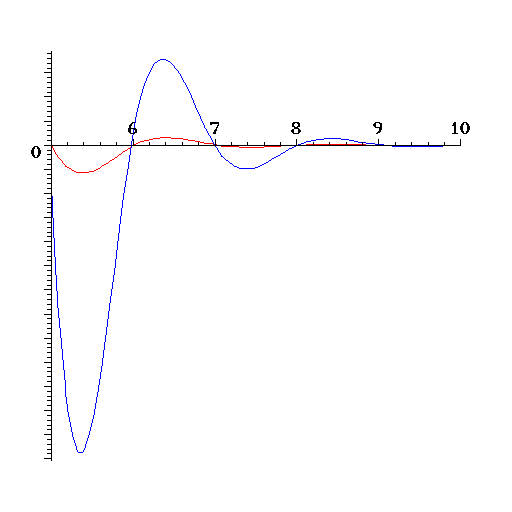
The speed of convergence of continued fractions to a number they represent
varies from number to number (but it is always very very fast). Here is
a comparison between the convergence errors for ![]() (blue) and
(blue) and ![]() (red).
(red).
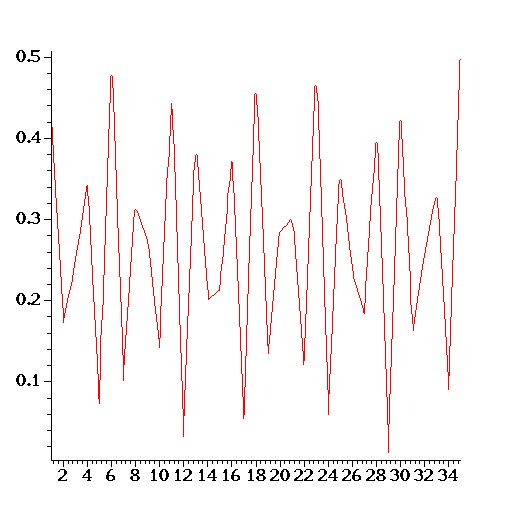
Definition 1
The fraction![]() is called a good approximation for
is called a good approximation for ![]() if for any
if for any ![]() and any integer
and any integer ![]() we have
we have ![]() .
.
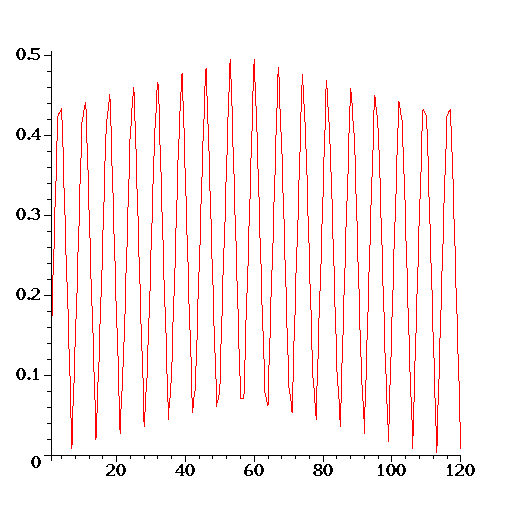
Observe that the numbers ![]() are exactly the denominators in the convergents for
are exactly the denominators in the convergents for ![]() and
and ![]() respectively. This is not an accident and holds in general for all convergents
and for all numbers
respectively. This is not an accident and holds in general for all convergents
and for all numbers ![]() .
We state it precisely and unambiguously in the form of a Theorem.
.
We state it precisely and unambiguously in the form of a Theorem.
THEOREM
1 Every convergent ![]() is a good approximation (in the sense of Definition 1) for
is a good approximation (in the sense of Definition 1) for![]() and conversely, every good approximation to
and conversely, every good approximation to ![]() is one of the numbers
is one of the numbers ![]() for some
for some ![]() .
In fact
.
In fact ![]() is the smallest integer
is the smallest integer ![]() such that
such that ![]() for some integer
for some integer ![]() .
We also have the inequalities
.
We also have the inequalities
Now that you know that continued fractions are very good at approximating numbers rational and irrational, it is not surprising to find them in many unusual (at first glance) places. Looking deeper at continued fractions you would discover many amazing properties of these objects. We can say that there is music in continued fractions. But also there are continued fractions in music. Armed with continued fractions we return to the calendar and discover how continued fractions can explain more or less any calendar system ever proposed or implemented.