Averaged Truncation and Optimal Prediction Methods
A fundamental problem in computational methods is the approximation of a system of evolution equations by a smaller system. The number of degrees of freedom in the original system may be too large for a direct computation (e.g. atoms in a crystal), or infinite (e.g. Fourier modes). The approximation typically consists of two parts. First, the degrees of freedom that are of interest (the resolved modes) have to be selected. Second, a system for those degrees has to be found, whose dynamics is close to the dynamics of the original (full) system. In many applications, the degrees of freedom have an obvious priority ranking, so the selection of resolved modes boils down to choosing a number of degrees. Then, the full system has to be truncated. A straightforward, but typically not very accurate, strategy is to simply neglect all unresolved degrees of freedom, or to set them to an equilibrium value.
One can do better by considering the unresolved degrees of freedom in an averaged fashion, as the method of optimal prediction does. In many applications, the dynamics possess an underlying measure (e.g. the grand canonical distribution in Hamiltonian molecular dynamics). Assume that the initial conditions of the resolved modes are known, while the unresolved degrees of freedom are sampled from the underlying measure (given the known initial conditions). Then an average solution of the full system can be defined, which is the mean over all solutions that start with the known initial conditions.
Typically, the computation of the average solution is as expensive as (or more expensive than) solving the full system. However, using a Mori-Zwanzig formalism, it can be approximated by a small system that uses only the resolved degrees of freedom. This small system consists of an averaged right hand side operator, plus a memory term, which is a convolution of a decaying kernel with the solution at former times. Suitable approximations to the memory term yield various versions of truncated systems. The strength of this approach is that it provides a systematic way to truncate a large system. Often times the fundamental approximation can be delayed to the very last step: the approximation of the memory term.
An application of this approach to a molecular dynamics system yields a boundary layer condition that acts as if a crystal were continued to infinity. An application to moment system for the equations of radiative transfer yields a new truncation approach. Existing truncations can be re-derived, and new ones are obtained, some of which improve the accuracy of approximation in example computations.
Molecular Dynamics
The diffusion of copper atoms in a silicon crystal due to atomic hopping is considered. Single copper atoms are trapped between a cell of silicon atoms. Due to random oscillations hopping events can occur, i.e. a copper atom jumps to a neighboring crystal cell. Copper shall be located near the surface of the silicon crystal. However, hopping can drive copper atoms deeper into the crystal, thus spoiling desired physical properties of the product. Direct molecular simulations can help understanding the nature of atomic hopping. Since only behavior near the surface of the crystal is of interest, in the direction normal to the surface, the computational domain has to be truncated at a certain distance.
A one dimensional model for a silicon crystal is constructed. While the potential between silicon atoms is singular (Lennard-Jones), the potential between silicon and copper is made finite, thus allowing hopping of copper over silicon.
The optimal prediction formalism, applied to the one dimensional molecular dynamics system, yields an evolution for the 24 silicon atoms closest to the crystal surface. The dependence on the other atoms deeper inside the crystal is averaged. Thus, the mean solution with respect to the grand canonical distribution is given by a high dimensional integration. Using an asymptotic expansion for low temperatures (solid state), this expression can be approximated by a high dimensional minimization problem: The low temperature limit of the mean solution behaves as if the unresolved atoms were following (without inertia) the potential minimum, given by the resolved atoms. Since the potential between two atoms reaches only over a few atomic distances, only a few virtual atoms have to be considered.
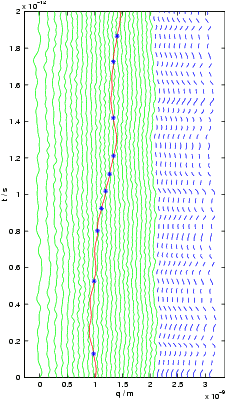
To the right, the time evolution of one copper atom (red path) in a crystal of silicon atoms (green paths) is shown. The temperature is significantly increased, so as to observe many hopping events (blue stars) in a reasonable time. The model is an averaged truncated model, derived from the optimal prediction formalism. The paths of ten virtual atoms (dashed blue lines) are shown, which follow the potential minimum generated by the resolved atoms.
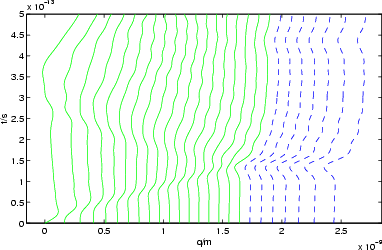
The optimal prediction system acts as if the crystal were continued to infinity, as long as the solution is in or near thermodynamical equilibrium. Non-equilibrium effects, such as sonic shock waves, are not treated correctly, as the figure on the left shows. A sonic wave is reflected at the artificial boundary between resolved and unresolved (virtual) atoms.
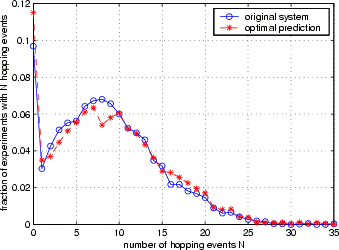
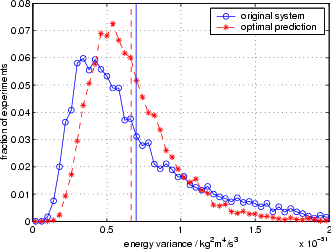
The copper diffusion can be used as a test for the quality of the optimal prediction truncation. The first figure on the right shows the number of hopping events for the full system (blue curve) and the truncated system (red curve). Apparently, the nature of atomic hopping is preserved well by the averaged truncation. On the other hand, the second figure on the right shows variance of the energy that is contained in the resolved atoms, as it fluctuates over time. This quantity is not preserved as well, indicating that the truncation creates an artificial boundary between resolved and virtual atoms, at which the nature of energy exchange is not reflected accurately. It is very likely that this observation is related to the artificial reflection of sonic waves.
Conclusion: The optimal prediction formalism yields a truncation of a large crystal in molecular dynamics simulations. In the low-temperature limit it yields a simple boundary layer condition that can be realized by a few virtual atoms. Equilibrium effects are reflected well, while non-equilibrium effects require more specific modeling.
Moment Methods for Radiative Transfer
As described in the section on research in radiative transfer, moment methods are based on a Fourier expansion of the solution of the radiative transfer equation in its angular variable. This expansion formally leads to an infinite system of macroscopic evolution equations for the moments. To allow a computation of the moment equations, this infinite coupled system must be truncated. How to do this best is the moment closure problem. Desired are suitable truncations, that approximate the full system of infinite moments by a system of only a few moments.
The optimal prediction formalism can be applied to the infinite moment system, transforming it into an integro-differential equation. A particular challenge is that the evolution happens in a function space (in the space variable), thus suitable measures have to be defined. Various approximations of the integral term yield different approximations:
- Dropping the integral term yields classical PN closures.
- Approximating the integral term over a finite time interval by a constant yields diffusion (N=0) and diffusion correction (N>0) closures.
- Approximating the integral term over an increasing time interval yields a new family of closure: The crescendo-diffusion approximations. The difference to classical diffusion (correction) approximations is that the diffusion is turned on slowly.
Test Problem in 1D
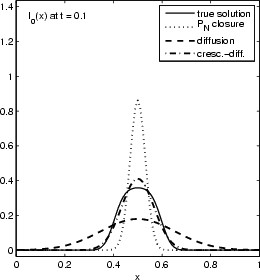
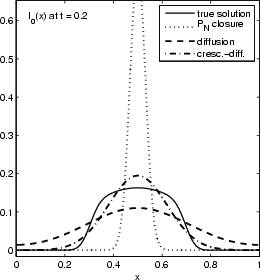
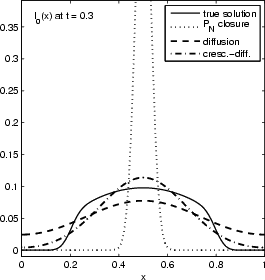
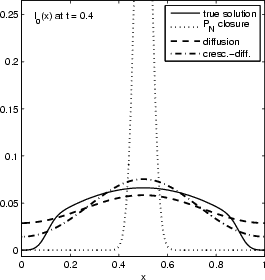
Considered is the source-free evolution of a chunk of photons initially localized near the origins, in a one dimensional slab geometry. Above figures show the time evolution of the energy distribution (lowest moment) of the true solution (solid graph), a P0 closure (dotted graph), a diffusion closure (dashed graph), and a crescendo diffusion closure (dash-dotted graph). While the diffusion approximation yields a significant improvement over the P0 system (which is a sole decay here), the crescendo diffusion approximation improves the quality of the results further. For short times, the pure diffusion closure is too diffusive, and the crescendo model remedies exactly this shortcoming by turning on the diffusion slowly with time, up to full diffusivity at t=0.33.
|
|
|
|
Test Problem in 2D
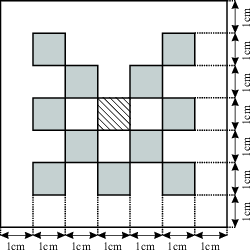
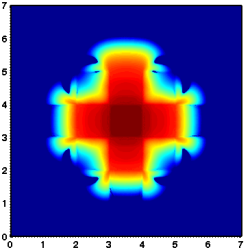
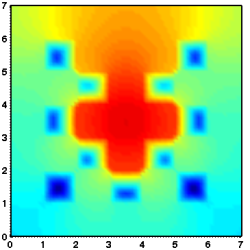
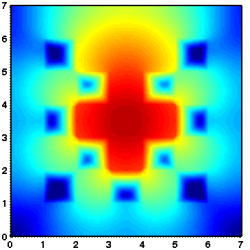
Considered is a two dimensional slab geometry with a checkerboard pattern (see figure one below) of two materials with different scattering and absorption properties. Initially, no photons are in the domain. At t=0, a constant source is turned on in the center. The true solution is shown in the second figure below. Results obtained by a classical diffusion approximation are shown in figure three below. In comparison, the results obtained by a crescendo diffusion approximation (shown in figure four below) are noticeably closer to the true solution.
|
|
|
|
| 2D lattice: geometry | 2D lattice: true solution | 2D lattice: diffusion approximation | 2D lattice: crescendo-diffusion |
Related Publications
| M. Frank, B. Seibold, Optimal prediction for radiative transfer: A new perspective on moment closure, Kinet. Relat. Models, Vol. 4, No. 3, 2011, pp. 717-733. |
| B. Seibold, M. Frank, Optimal prediction for moment models: Crescendo diffusion and reordered equations, Continuum Mech. Thermodyn., Vol. 21, No. 6, 2009, pp. 511-527. |
| B. Seibold, Optimal prediction in molecular dynamics, Monte Carlo Methods Appl., Volume 10, Number 1, 2004, pp. 25-50. |